Cylinder
(L>>r)
次には並進から.
| Parameter | Direction | Cylinder |
 |
||
| \(\Large \gamma_{ \parallel }\) | |
\(\Large \frac{2 \pi \eta L}{ln(L/(2r))-0.20} \) |
| \(\Large \gamma_{ \perp } \) |  |
\(\Large \frac{4 \pi \eta L}{ln(L/(2r))+0.84} \) |
並進の場合にも分母にlnが入っているので,L≒rの場合にはこの式は適用できないことになります.
元論文は,
Translational friction coefficients of rigid, symmetric top macromolecules. Application to circular cylinders
Maria M. Tirado and José García de la Torre
J. Chem. Phys. 71, 2581 (1979)
です.Table I.,に,
p-1 |
γ⊥ |
γ∥ |
0.50 |
0.99 |
0.25 |
0.46 |
0.97 |
0.21 |
0.42 |
0.96 |
0.18 |
0.38 |
0.94 |
0.14 |
0.33 |
0.92 |
0.10 |
0.30 |
0.91 |
0.07 |
0.25 |
0.90 |
0.03 |
0.20 |
0.88 |
-0.02 |
0.17 |
0.87 |
-0.05 |
0.10 |
0.86 |
-0.11 |
0.06 |
0.85 |
-0.15 |
0.02 |
0.84 |
-0.18 |
0 |
0.84 |
-0.20 |
なる表があります.
\(\Large p = L/(2r) \)
と定義されていますので,Lが十分長い場合(p-1=0)には上記式の分母の係数,長軸方向の場合の-0.20,短軸方向の場合の0.84,と一致します.
このテーブルの関係は,
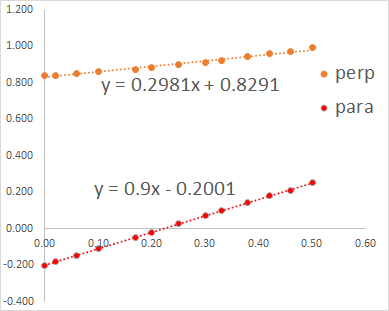
と直線関係になるので,上記の式を変形してみましょう.すると,
\(\Large \gamma_{ \parallel } = \frac{2 \pi \eta L}{ln(L/(2r)) + 0.9 \frac{2r}{L} -0.20} \)
\(\Large \gamma_{ \perp } = \frac{4 \pi \eta L}{ln(L/(2r)) + 0.2981 \frac{2r}{L} +0.8291} \)
となります.この式を描いてみると,
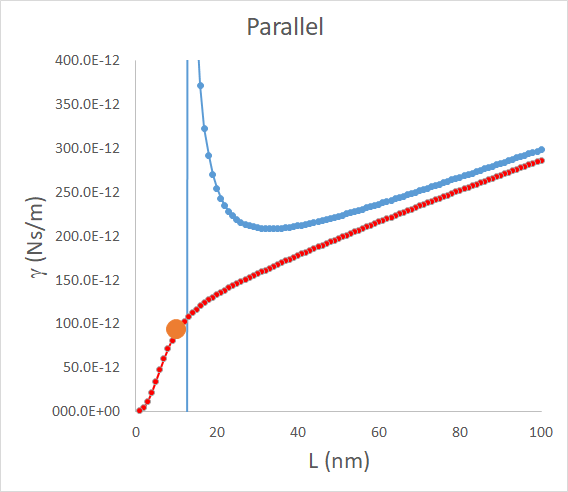
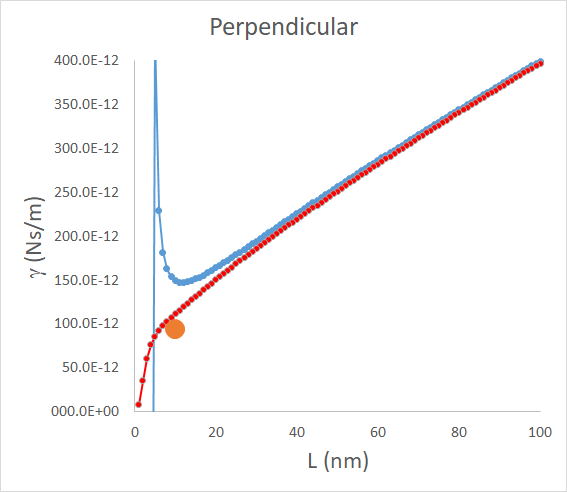
となり,かなりいい感じとなります.
先に述べましたように,たぶんこの論文に描かれているこの表は理論的・実験的な根拠があるわけではなく,多項式近似式を当てはめただけと思いますので,便宜上と思われます.
これでとりあえずはアスペクト比の小さい円柱の場合の粘性抵抗係数を見積もることが可能となります.
きちんと計算したわけではありませんが,元となるナビエ-ストークスの法則自体が近似値なので,厳密解というよりはオーダーレベルの議論にとどめておいた方がよいかと思います.